【情報工学基礎】加算器とは?(初心者向け) 基本的に、わかりやすく説明
電気を利用し計算を行う電子計算機やコンピュータ、その内部では電気を0と1の2進数で論理的に処理し計算しています。
今回は、その計算や処理方法を基本的な考えで解説します。
論理演算
論理演算とは、ある事象(状態)が、「真」または「偽」を 判断する演算のことです。
電子計算機やコンピュータの細部(以降、コンピュータと略します)は、それらの情報(真、偽)を「0」と「1」て扱い、その論理演算結果も必ず「0」、「1」で処理します。
論理回路
コンピュータは、2進数値「0」、「1」に伴って、AND、OR、NOTなどの論理演算で,データとして計算して処理されています。
計算処理として「四則演算」加・減・乗・除を行っているように見えますが、実際には論理演算が行われています。
基本は足し算
足し算(加算)の回路が出来れば、その加算回路を応用とし四則演算が実現できます。
。
加算(+)
「加算」が最も基本。 減算(引き算)、乗算(掛け算)、除算(割り算)は、足し算の応用形になりえます。
減算(-)
補数(マイナスの数)を加算すれば、減算となる。
乗算(×)
繰返し加算すれば、乗算となる。
除算(÷)
減算を繰返しその計数が、除算となる。
加算器とは
「加算処理を行う演算装置」 2進数で足し算を行う回路のことを、加算器と言い、
具体的には、AND回路、OR回路、XOR回路に伴う論理回路の組合わせで構成されています。
加算器は、半加算器と全加算器の2種類があります。
半加算器
半加算器(Half Adder)は、一桁同士の足し算を行う加算器です。
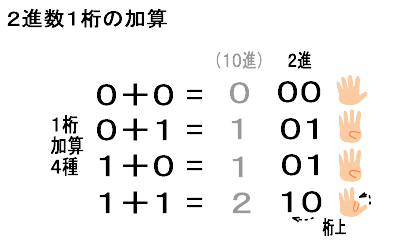
足される元数を「A」、足す数を「B」をそれぞれ、
加算結果S(加算:Sum)、桁上げC(繰り上げ)にて、真理値表として表現し
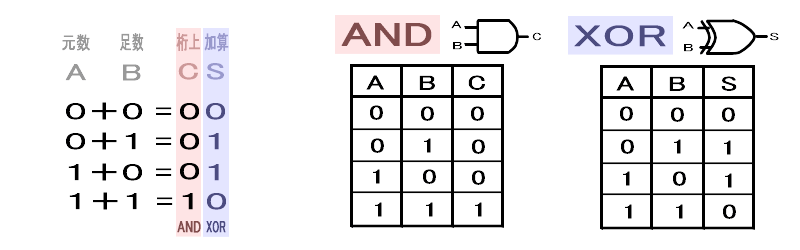
論理回路として考察してみると、
- AND「論理積」
両方の入力が1の場合に1を出力する回路 - XOR「排他的論理和」
両方の入力が同じ場合は0を、異なっている場合は1を出力する回路
半加算器は、この回路の組合せで構成され、加算処理が実行されます。

処理結果に伴う「桁上」は、それを信号として通知が可能ですが、
逆に、性質上(1桁縛り)によって、他からの桁上げ信号を受取る(意識する)ことができません。
したがって、「半加算器」は1桁のみの加算器として成り立っています。
全加算器
全加算器(Full Adder)は、桁上げ(信号入力)が意識できる 加算演算機能が加わった加算器です。
桁上げ信号を下位から受取り、その演算結果に伴う桁上信号も上位に通知できます。
入力(A)、(B)及び下位からの(Ci)の3つ入力データで加算処理を行い、
加算結果(S)と、上位への桁上げ信号(Co)の2つを出力します。
その構図と真理値表は、
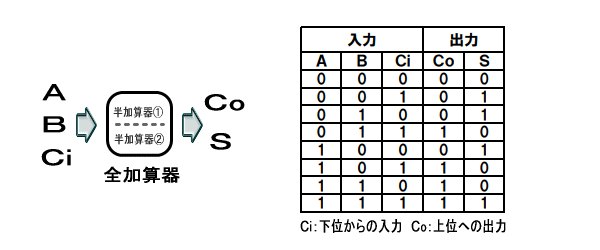
入力A と 入力Bを 半加算器①にて加算
結果S と 下位からのCi を半加算器②にて加算
その結果が全加算器のSになります。

なお、全加算器は、半加算器①、②それぞれのCを、「OR」演算結果した結果が上位へのCoとなります。(つまり、半加算器①、② のいずれかの桁上げを 「OR」演算にて処理します)
複数ビットの加算
複数ビットの加算とは、加算するその桁数をビット数として表しています。
1桁の加算は1ビット加算、2桁の加算は2ビット・・・n桁の加算はnビットと表現されています。
複数ビットの加算は、加算回路の組合せで実現できます。
- 1ビット
半加算回路(桁意識なし)(例:0+1=1等)
全加算回路(桁意識あり)(例:1+1=10等) - 2ビット
半加算回路(1ビット) + 全加算回路(1ビット)
(2ビット例:10+01 = 11等) - nビット
半加算回路(1ビット) + n(-1)個の連結全加算回路
(4ビット例:1001+0010=1011等)
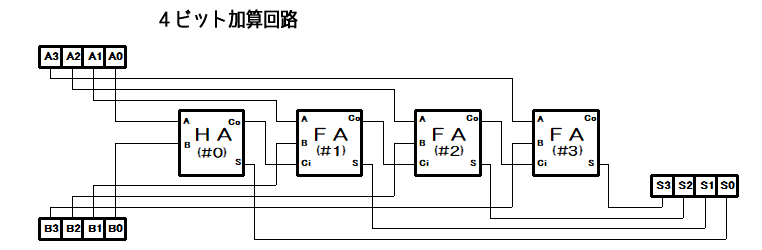
具体的には、複数ビットの加算回路は 加算器間の桁上げ信号の連結で構成されています。
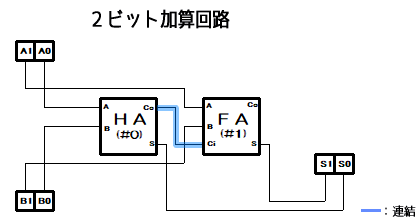
まとめ
- 加算器とは、2進数で足し算を行う回路
- 1桁で桁意識の無い半加算器(Half Adder)と2桁以上の全加算器(Full Adder)の2種類がある。
- 加算器を複合することによって、複数ビットでの演算ができる。
